De la notation infixée vers la notation postfixée

publication: 20 octobre 2022 / mis à jour 20 octobre 2022

Read this page in english

Appel à collaboration

Vous développez des montages, simples ou complexes avec ESP32 et ESP32forth.

Partagez-les ici sur ce site.

ESP32forth ne pourra se développer qu'avec la collaboration active de toutes les bonnes volontés.

Vos montages peuvent aider d'autres développeurs.

Les montages des autres développeurs peuvent vous aider.

Pour proposer un article ou un montage, cliquez ici

Les notations préfixées, infixées et postfixées

Le langage FORTH utilise une notation dite postfixée appellée aussi notation RPN. La notation RPN permet de se passer des parenthèses utilisées en notation infixée:

notation infixée: ( 2 + 3 ) * 2
notation postfixée: 2 3 + 2 *

La notation dite préfixée est utilisée par certains langages, tel LISP:

notation préfixée: (* 2 (+ 2 3 ) )

Pour FORTH, le problème est de trouver une méthode fiable pour convertir les formules arithmétiques classiques, dites infixées, en notation postfixée exploitable par FORTH.

De ce problème est née l'idée de créer un programme - en FORTH - pour effectuer cette conversion.

Le programme de conversion infixée vers postfixée

Le programme initial a été développé pour fonctionner avec TURBO-Forth sous MS-DOS.

Version originale:

CREATE OP 44 ALLOT
: ?INTERP ( PFA ---)  STATE @ IF , ELSE EXECUTE THEN ;
: OPP@    ( --- ADR)  OP DUP @ + ;
: >OP     ( PFA NIVEAU ---) 4 OP +! OPP@ 2! ;
: OP>     ( ---)  OPP@ 2@ -4 OP +! DROP ?INTERP ;
: LEV?    ( --- NIVEAU)  OPP@ @ ;
: ]$ BEGIN LEV? WHILE OP> REPEAT FORTH ; IMMEDIATE
 
: TRAITE  ( PFA --- ) 2@
BEGIN   DUP LEV? > NOT
WHILE   >R >R OP> R> R>  REPEAT >OP ;
 
: INFIX   ( N --- <MOT> <MOT>   EN COMPILATION )
' CREATE SWAP , , IMMEDIATE
DOES>  TRAITE ;
 
VOCABULARY ALGEBRE    ALGEBRE DEFINITIONS
7 INFIX * *    7 INFIX / /    6 INFIX + +    6 INFIX - -
5 INFIX > >    5 INFIX < <    5 INFIX = =
4 INFIX NOT NOT 3 INFIX AND AND 2 INFIX OR OR
 
: ( ['] CR 1 >OP ; IMMEDIATE
 
: ) [ FORTH ] BEGIN 1 LEV? < WHILE OP> REPEAT
  1 LEV? = IF -4 OP +! ELSE TRUE ABORT" MANQUE (" THEN ;
IMMEDIATE
FORTH DEFINITIONS
 
: $[ OP 44 0 FILL ALGEBRE ; IMMEDIATE

Cette version a été écrite en 1987.

La version actuelle a été réécrite et adaptée pour être compilée par ESP32forth.

La pile des opérateurs

Afin de gérer la priorité dand l'ordre d'exécution des opérateurs infixés et les imbrications des parenthèses, il est nécessaire de gérer ces opérateurs dans une pile nommée op:

DEFINED? --infix [if] forget --infix  [then] 
create --infix 
 
\ Define operator stack 
80 constant OPERATORS         \ increase value 80 if needed 
cell 2* OPERATORS * constant OP-SIZE 
create op               \ operator stack 
    OP-SIZE allot 
 
\ pointer for operator pointer 
0 value op-pointer 
 
\ get current operator pointer 
: opp@    ( --- addr ) 
    op op-pointer + 
  ; 
 
\ increase operator pointer 
: opp+ ( -- ) 
    cell 2* +to op-pointer 
  ; 
 
\ decrease operator pointer 
: opp- ( -- ) 
    cell 2* negate +to op-pointer 
  ; 
 
\ execute or compile word 
: ?interp ( cfa -- ) 
    state @             \ 0 = interpret mode, -1 = compile mode 
    if      ,           \ compile word 
    else    execute     \ execute word 
    then 
  ; 
 
\ store cfa and level on operator staock 
: >op     ( cfa level -- ) 
    opp+ 
    opp@ 2! 
  ; 
 
\ get cfa from operator stacl 
: op>     ( -- ) 
    opp@ 2@ 
    opp- 
    swap drop ?interp 
  ;

Le pointeur de pile est stocké dans la première cellule de cette pile op. Le poointeur est incrémenté par opp+ et décrémenté par opp-.

Le mot opp@ restitue l'adresse réelle dans la pile op pointée par le pointeur de pile.

Le mot >op incrémente le pointeur de pile op et stocke l'opérateur à mettre en attente et son niveau.

Le mot op> récupère l'opérateur en attente et son niveau. Le pointeur de pile op est ensuite décrémenté puis l'opérateur est exécuté ou compilé.

Définition des opérateurs infixés

\ get level pointed by current operator stack 
: lev?    ( -- level ) 
    op-pointer op + @ 
  ; 
 
\ end an algebric formula 
: ]$ 
    begin   lev? 
    while   op> 
    repeat 
    forth ; immediate 
 
\ execute part of algebra operator 
: dealing  ( addr --- ) 
    2@ 
    begin   over lev? > invert 
    while   >r >r op> r> r> 
    repeat 
    >op 
  ; 
 
\ define algebra operator. 
: infix   ( n ---     in compilation ) 
    '               \ get cfa word1 
    create          \ create word2 
        swap , , 
        immediate 
    does> 
        dealing 
  ; 
 
vocabulary algebra    algebra definitions 
7 infix * *    7 infix / / 
6 infix + +    6 infix - - 
5 infix > >    5 infix < <    5 infix = = 
4 infix invert not 
3 infix and and 
2 infix or or

Le mot ]$ ferme une séquence arithmétique infixée. Ce mot boucle tant que la pile op n'est pas vide.

Le mot infix est un mot de définition permettant de créer les opérateurs infixés dans le vocabulaire algebra. Syntaxe de définition d'un opérateur infixé: n infix <word1> <word2>:

n est le niveau de l'opérateur
<word1> est le mot à exécuter quand la formule infixée sera exécutée ou compilée
<word2> est le mot à créer dans le vocabulaire algebra

Définition des parenthèses

: noop ; 
 
: ( 
    1  ['] noop >op 
  ; immediate 
 
: ) 
    [ forth ] 
    begin   1 lev? < 
    while   op> 
    repeat 
    1 lev? = 
    if    opp- 
    else  ." miss " 40 emit space 
          -1 throw 
    then 
  ; immediate

Les mots ( et ) sont eux aussi compilés dans le vocabulaire algebra. Le mot ( dans le vocabulaire algebra fonctionne comme un opérateur de niveau 1. La compilation du mot noop sert simplement à stocker un mot neutre lequel ne sera pas executé.

Le mot ) du vocabulaire algebra traite la section de formule marqué par (. Exemple: $[ ( 2 + 3 ) ]$

Ouverture d'une séquence arithmétique infixée

\ start algebric formula 
forth definitions 
: $[ 
    op OP-SIZE 0 fill 
    0 to op-pointer 
    algebra 
  ; immediate

Le mot $[ ouvre une séquence arithmétique infixée qui s'achève par le mot ]$.

Exemple:

: ex1 ( --- n) 
    $[ ( ( 2 + 3 ) * ( 4 + 1 ) ) ]$ 
    \ two 3 + 4 1 + * 
  ;

Utilisation pratique

Le code complet est disponible ici: infix.txt

Il doit être compilé avec ESP32forth.

Une fois compilé, testez l'exemple ex1:

: ex1 ( --- n)  compiled 
    $[ ( ( 2 + 3 ) * ( 4 + 1 ) ) ]$  compiled 
  ;  ok 
  ok 
see ex1 
: ex1 
  2 3 + 4 1 + * ; ok

La séquence see ex1 permet de décompiler notre exemple ex1. Dans cette décompilation, on constate que notre expression algébrique
( ( 2 + 3 ) * ( 4 + 1 ) )
est devenue:
2 3 + 4 1 + *

Utilisation de variables

Dans une expression infixée, on peut utiliser des variables de type values. Exemple:

0 value X 
0 value A 
0 value B 
0 value C 
: toABCX ( a b c x ---) 
    to X 
    to C 
    to B 
    to A 
  ; 
: ex2 ( --- n) 
    $[ ( A * ( X * X ) ) + ( B * X ) + C ]$ 
  ;

La décompilation de ex2 donne A X X * * B X * + C +.

Utilisation:

1 1 1 2 toABCX  ok 
ex2  ok 
.s <1> 7  ok

Expressions logiques

On peut également traiter des expressions logiques:

: toABC ( a b c ---) 
    to C 
    to B 
    to A 
  ; 
: ex3 ( --- fl ) 
    $[  ( not A and C ) or ( B and not C ) or ( A and not B )  ]$ 
  ;

La décompilation de ex3 donne A invert C and B C invert and or A B invert and or

Voici un exemple qui mélange expressions arithmétiques et logiques. Cet exemple se propose de convertir une température de degrés Celsius en degrés Kelvin ou Fahrenheit:

0 value KELVIN 
0 value FAHRENHEIT 
0 value tempCelsius 
: toK ( ---) 
    false to FAHRENHEIT 
    true  to KELVIN 
  ; 
: toF ( ---) 
    false to KELVIN 
    true  to FAHRENHEIT 
  ; 
: C. ( deg --- deg2) 
    to tempCelsius 
    $[ 
        ( ( tempCelsius + 273 ) and KELVIN )   + 
        ( ( ( tempCelsius * 9 / 5 ) + 32 ) and FAHRENHEIT ) 
    ]$ 
    .   \ display result 
  ;

Dans cette séquence ( tempCelsius + 273 ) and KELVIN on convertit les degrés Celsius en degrés Kelvin. La variable KELVIN contient un flag booléen: s'il est nul, le résultat de la conversion sera nul. Dans le cas contraire le résultat correspondra au calcul. Le procédé est le même sur la ligne suivante, où on fait un and logique avec le résultat en degrés Fahrenheit.

Exemple d'utilisation:

10 ToF C. 42  ok
10 toK C. 283  ok

Voici le résultat de la décompilation de notre formule dans C.:
tempCelsius 273 + KELVIN and tempCelsius 9 * 5 / 32 + FAHRENHEIT and +

Si on veut réutiliser cette portion de code décompilé sur ESP32forth, on pourra écrire notre code ainsi:

0 value KELVIN 
0 value FAHRENHEIT 
0 value tempCelsius 
: toK ( ---) 
    false to FAHRENHEIT 
    true  to KELVIN 
  ; 
: toF ( ---) 
    false to KELVIN 
    true  to FAHRENHEIT 
  ; 
: C. ( deg --- deg2) 
    to tempCelsius 
    tempCelsius 273 + KELVIN and 
    tempCelsius 9 * 5 / 32 + FAHRENHEIT and  + 
    .   \ display result 
  ;

De la notation infixée vers la programmation linéaire

La notation infixée est l'occasion de montrer un aspect intéressant des opérations en mixant opérateurs algébriques et opérateurs logiques.

Pour ce faire, on part d'un challenge consistant à programmer des opérations permettant de restituer cette image sous ESP32forth:

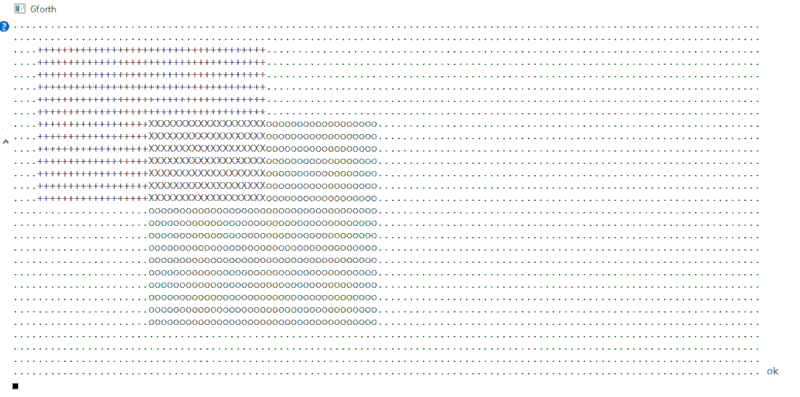
Dans un cadre de 120 colonnes sur 30 lignes, on affiche deux rectangles:

le premier rectangle est rempli avec des caractères "+", le second avec des caractères "o"
à l'intersection de ces deux rectangles, on remplit avec des caractères "X"
en dehors de ces deux rectangles, on remplit avec le caractère "."

Comment gérer la sélection du caractère à afficher uniquement en utilisant des formules arithmétiques et logiques?

Affichage et gestion du contenu des rectangles

Dans un espace quelconque, ici un écran en mode texte, on doit afficher deux rectangles:

Nous sommes en mode texte. Le curseur ne peut être positionné sur notre espace d'affichage qu'en affichant un caractère dans une ligne, puis en passant à la ligne suivante.

Selon sa position, le curseur doit afficher un de ces quatre caractères: . + X et o. Dans la figure ci-dessus, la position du curseur est pointé par deux variables DX et DY.

Le programme doit émettre 120 caractères par ligne, ce sur 30 lignes.

0 value DX      \ current X coordinate 
0 value DY      \ current Y coordinate 
 
: dx+  ( ---)   \ increment DX 1 position 
    DX 1+ to DX ; 
 
: dy+  ( ---)   \ increment DY 1 position 
    DY 1+ to DY ;

Les variables DX DY mémorisent la position du curseur. Le contenu de ces variables est géré comme suit:

à chaque caractère émis, on incrémente DX avec le mot dx+
à la fin de chaque ligne, on remet à zéro le contenu de DX et on incrémente le contenu de DY avec le mot dy+

Traitement logique de la position du curseur

Les dimensions d'un rectangle sont déterminées par quatre variables SX EX SY EY (SX pour Start X...):

0 value SX    \ x Start rect 1 
0 value EX    \ x End   rect 1 
0 value SY    \ y Start rect 1 
0 value EY    \ y End   rect 1

Il faut donc déterminer si la position du curseur est située dans un rectangle. Voici la formule logique délivrant un flag booléen en fonction de la position du curseur:

( NOT ( DX < SX ) ) AND ( NOT ( DX > EX ) ) AND ( NOT ( DY < SY ) ) AND ( NOT ( DY > EY ) )

Voyons en détail le premier membre de cette formule logique:

( NOT ( DX < SX ) )

Pour savoir si DX est à l'intérieur d'un rectangle, nous avons deux possibilités:

en formulant par inclusion: DX >= SX. Seul souci, l'opérateur >= n'est pas défini dans le fichier infix.txt
en formulant par exclusion: NOT ( DX < SX). Cette solution convient car > est défini dans le fichier infix.txt

Voici le codage de cette formule grâce à la notation infixée:

: inRect? ( --- fl) 
    $[      ( NOT ( DX < SX  ) ) AND 
            ( NOT ( DX > EX  ) ) AND 
            ( NOT ( DY < SY  ) ) AND 
            ( NOT ( DY > EY  ) ) 
    ]$  ;

Le mot inRect? va délivrer un flag booléen si DX DY est dans le rectangle dont la dimension est indiquée par le contenu des variables SX EX SY EY.

Une fois compilé, on peut regarder ce qu'est devenue notre formule infixée en tapant see inRetc? depuis l'interpréteur FORTH, ce qui nous affiche ceci:

see inRect? 
: inRect? 
  DX SX < invert DX EX > invert and DY SY < invert and DY EY > invert and ; ok

La compilation d'une formule en notation infixée restitue un code FORTH parfaitement optimisé!

Traitement des différents cas logiques

Nous allons maintenant aborder les différentes situations logiques permettant de sélectionner le caractère à afficher. Pour ce faire, nommons leftRect le rectangle de gauche, puis rightRect le rectangle de droite. On peut déjà définir deux mots restituant un flag booléen si le curseur se trouve dans un de ces deux rectangles:

: inLeftRect? ( --- fl) 
    4  to SX    \ x Start rect left 
    40 to EX    \ x End   rect left 
    4  to SY    \ y Start rect left 
    16 to EY    \ y Etart rect left 
    inRect?  ; 
 
: inRightRect? ( --- fl) 
    22 to SX    \ x Start rect right 
    58 to EX    \ x End   rect right 
    10 to SY    \ y Start rect right 
    26 to EY    \ y Etart rect right 
    inRect?  ;

Avec ces paramètres, nos deux rectangles partagent une zone commune. Nous verrons plus loin comment traiter ce cas.

Le curseur d'affichage doit donc gérer quatre situations:

si le curseur n'est pas dans leftRect et rightRect, on affiche le caractère "."
si le curseur est dans leftRect mais n'est pas dans rightRect, on affiche le caractère "+"
si le curseur n'est pas dans leftRect mais est dans rightRect, on affiche le caractère "o"
si le curseur est dans leftRect et dans rightRect, on affiche le caractère "X"

Prenons le premier cas: le courseur n'est pas dans leftRect et rightRect.

La partie de formule logique sera de la forme:
( NOT inLeftRect? ) AND ( NOT inRightRect? )

Cette partie de code va restituer un flag booléen dont la valeur numérique sera 0 ou -1.

Si on exécute le mot abs à ce flag booléen, on aura deux résultats: 0 ou 1
( NOT inLeftRect? ) AND ( NOT inRightRect? ) abs

Le code ASCII du caractère "." est 46. On multiplie ce code ASCII par le résultat de notre formule:
46 * ( ( ( NOT inLeftRect? ) AND ( NOT inRightRect? ) ) abs )

Mettons cette formule dans un nouveau mot:

: dispChar ( -- ) 
    $[    \ 46  is char . 
            46  * ( ( ( NOT inLeftRect? ) AND ( NOT inRightRect? ) ) abs 
    ]$ 
    emit 
  ;

Prenons le second cas: le courseur est dans leftRect mais n'est pas dans rightRect.

La partie de formule logique sera de la forme:
( inLeftRect? ) AND ( NOT inRightRect? )

Dans ce second cas, le code ASCII du caractère "+" est 43. On multiplie ce code ASCII par le résultat de notre formule:
43 * ( ( ( inLeftRect? ) AND ( NOT inRightRect? ) ) abs )

Nous avons maintenant deux formules, lesquelles restituent soit 0, soit le code ASCII du caractère à afficher. Notre mot dispChar devient:

: dispChar ( -- ) 
    $[    \ 46  is char . 
          ( 46  * ( ( ( NOT inLeftRect? ) AND ( NOT inRightRect? ) ) abs ) ) 
          \ 43  is char + 
        + ( 43  * ( ( ( inLeftRect? ) AND ( NOT inRightRect? ) ) abs ) ) 
    ]$ 
    emit 
  ;

Nous avons déjà deux situations: 46 + 0 ou 0 + 43...

Il reste deux cas à traiter. Voici la définition complète du mot dispChar prenant en compte tous les cas:

: dispChar ( -- ) 
    $[    \ 46  is char . 
          ( 46  * ( ( ( NOT inLeftRect? ) AND ( NOT inRightRect? ) ) abs ) ) 
          \ 43  is char + 
        + ( 43  * ( ( ( inLeftRect? ) AND ( NOT inRightRect? ) ) abs ) ) 
          \ 88  is char X 
        + ( 88  * ( inLeftRect? AND inRightRect? abs ) ) 
          \ 111 is char o 
        + ( 111 * ( ( ( inRightRect? ) and ( NOT inLeftRect? ) ) abs ) ) 
    ]$ 
    emit 
  ;

Dans cette définition, on restitue un seul caractère ASCII dont le code est adapté à la position du curseur, tout ceci sans aucun test if..then ou équivalent.

Voici ce que donne la décompilation du mot dispChar:

see dispChar 
: dispChar 
  46 inLeftRect? invert inRightRect? invert and abs * 43 inLeftRect? 
  inRightRect? invert and abs * + 88 inLeftRect? inRightRect? abs and * + 111 
  inRightRect? inLeftRect? invert and abs * + emit ; ok

Boucles d'affichage

Dans le mot graphLoop nous gérons deux boucles imbriquées. Dans la boucle intérieure, on traite l'affichage du caractère avec le mot dispChar puis on incrémente la valeur de DX avec le mot dx+.

Dans la boucle extérieure, on incrémente la valeur de DY avec le mot dy+ puis on remet à zéro le contenu de DX:

: graphLoop ( ---) 
    30 for 
        cr 
        120 for 
            dispChar 
            dx+ 
        next 
        dy+ 
        0 to DX 
    next ;

Conclusion

La conversion d'expressions arithmétiques infixées en expressions postfixées permet de convertir sans erreur des expressions arithmétiques ou logiques complexes.

Avec ESP32forth, on compilera des expressions infixées, puis en récupérant la décompilation de ces expressions, on pourra les utiliser sur d'autres versions de Forth, en particulier sur ESP32forth qui n'intègre pas d'origine la notion de vocabulaire.

ESP32forth intègre les nombres réels (à virgule flottante). Il est donc possible de créer une variante de ces routines pour traiter les nombres réels. Si vous réalisez cette variante, contactez-moi pour une éventuelle publication.

Legal: site web personnel sans commerce / personal site without seling

Autres articles / Other articles