Synthèse sonore avec ESP32Forth
publication: 20 juillet 2022 / mis à jour 10 août 2022
Appel à collaboration
Vous développez des montages, simples ou complexes avec ESP32 et ESP32forth.
Partagez-les ici sur ce site.
ESP32forth ne pourra se développer qu'avec la collaboration active de toutes les bonnes volontés.
Vos montages peuvent aider d'autres développeurs.
Les montages des autres développeurs peuvent vous aider.
Pour proposer un article ou un montage, cliquez ici
Pré-requis
Pour vos premières expérimentations sonores, il faut disposer d'un haut-parleur que vous connectez à une sortie GPIO. Mais l'impédance des haut-parleurs étant très basse, il faudra passer par un transistor. Voici le schéma conseillé pour un petit haut-parleur:
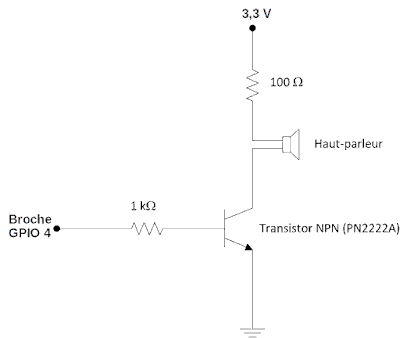
Sur ce schéma, il est mentionné le pin GPIO4. En fait, ce montage est utilisable sur n'importe quelle sortie GPIO de la carte ESP32. Les deux sorties qui vont plus particulièrement nous intéresser sont GPIO25 et GPIO26 qui sont réservées aux sorties DAC (Digital to Analog Conversion).
Synthèse sonore simple
Pour ce premier article, nous allons utiliser la génération de signaux PWM, mais sur les sorties DAC.
Notre buzzer est connecté à la sortie GPIO25, via le transistor PN2222A qui sert d'adapteur d'impédance.
0 constant CHANNEL0 \ define PWM channel 0 25 constant BUZZER \ buzzer connected to GPI25 ledc \ select ledc vocabulary : initTones ( -- ) BUZZER CHANNEL0 ledcAttachPin ;
Le mot initTones connecte la sortie GPIO25 au canal PWM 0. La génération d'un son s'effectue selon:
CHANNEL0 freq ledcWriteTone drop
où freq est la fréquence souhaitée, multipliée par 1000. Ainsi, pour générer la note LA (A en notation anglaise), dont la fréquence est de 440 Hz, il faudra utiliser la valeur 440*1000:
CHANNEL0 440000 ledcWriteTone drop
Définition du tableau des fréquences sonores
Pour retrouver les fréquences sonores des notes de musique, nous sommes allés sur Wikipedia. On construit
un tableau des fréquences, où chaque fréqence sera enregistrée sous sa forme utilisable par ledcWriteTone:
\ frequency notes \ source: https://fr.wikipedia.org/wiki/Note_de_musique \ frequency is multiplied by 1000 create NOTES \ C C# D D# E F F# G G# A A# B \ octave -1 15350 , 17330 , 18360 , 19450 , 20600 , 21830 , 23130 , 24500 , 25960 , 27500 , 29140 , 30870 , \ octave 0 32700 , 34650 , 36710 , 38890 , 41200 , 43650 , 46250 , 49000 , 51910 , 55000 , 58270 , 61740 , \ octave 1 65410 , 69300 , 73420 , 77780 , 82410 , 87310 , 92500 , 98000 , 103830 , 110000 , 116540 , 123470 , \ octave 2 130810 , 138590 , 146830 , 155560 , 164810 , 174610 , 185000 , 196000 , 207650 , 220000 , 233080 , 246940 , \ octave 3 261630 , 277180 , 293660 , 311130 , 329630 , 349230 , 369990 , 392000 , 415300 , 440000 , 466160 , 493880 , \ octave 4 523250 , 554370 , 587330 , 622250 , 659260 , 698460 , 739990 , 783990 , 830610 , 880000 , 932330 , 987770 , \ octave 5 1046500 , 1108730 , 1174660 , 1244510 , 1318510 , 1396910 , 1479980 , 1567980 , 1661220 , 1760000 , 1864660 , 1975530 , \ octave 6 2093000 , 2217460 , 2349320 , 2489020 , 2637020 , 2793830 , 2959960 , 3135960 , 3322440 , 3520000 , 3729310 , 3951070 , \ octave 7 4186010 , 4434920 , 4698640 , 4978030 , 5274040 , 5587650 , 5919910 , 6271930 , 6644880 , 7040000 , 7458620 , 7902130 , \ octave 8 8372020 , 8869840 , 9397280 , 9956060 , 10548080 , 11175300 , 11839820 , 12543860 , 13289760 , 14080000 , 14917240 , 15804260 ,
Il y a douze notes par octave, d'où la définition de 12 valeurs par ligne. Ici, on enregistre seulement 10 lignes, soit 10 octaves. Car passé 15Khz, les sons ne seraient plus audibles.
Pour retrouver une note, il suffit de connaitre sa position dans une octave. Par exemple, notre note LA en octave 3 sera: ((octave+1)*12)+position. LA étant en 10ème position en octave 3, l'adresse à déterminer sera NOTES+4*((OCTAVE+1*12)+position)
Récupération de la fréquence d'une note de musique
On crée d'abord un mot set.octave qui nous permettra de sélectionner l'octave souhaitée. Ensuite, on définit
get.note qui récupère la fréquence de la note souhaitée:
3 value OCTAVE \ select octave in interval -1..8 : set.octave ( n[-1..8] ) to OCTAVE ; \ select note in interval 1..12 : get.note ( n[1..12] -- ) 1- OCTAVE 1+ 12 * + cell * \ calc. offset in NOTES array NOTES + @ \ fetch frequency of selected note ; 3 value OCTAVE \ select octave in interval -1..8 : set.octave ( n[-1..8] ) to OCTAVE ; : OCT6 ( -- ) 6 set.octave ; : OCT5 ( -- ) 5 set.octave ; : OCT4 ( -- ) 4 set.octave ; : OCT3 ( -- ) 3 set.octave ; : OCT2 ( -- ) 2 set.octave ; : OCT1 ( -- ) 1 set.octave ;
Nous verrons plus loin comment gérer les notes en les appelant depuis leur notation.
Gestion de la durée des notes
La durée d'une note, c'est l'intervalle de temps qui sépare le déclenchement de deux notes consécutives.
Un délai de base est défini par la constante WHOLE-NOTE-DURATION.
Les durées sont définies dans un nouveau vocabulaire music:
1600 constant WHOLE-NOTE-DURATION WHOLE-NOTE-DURATION value duration vocabulary music music definitions music also \ set duration of a whole note : o ( -- ) WHOLE-NOTE-DURATION to duration ; \ set duration of a white note : o| ( -- ) WHOLE-NOTE-DURATION 2/ to duration ; \ set duration of a black note : .| ( -- ) WHOLE-NOTE-DURATION 2/ 2/ to duration ; \ set duration of a half black note : .|' ( -- ) WHOLE-NOTE-DURATION 2/ 2/ 2/ to duration ; \ set duration of a quarter black note : .|" ( -- ) WHOLE-NOTE-DURATION 2/ 2/ 2/ 2/ to duration ;
On définit des mots qui symbolisent les durées souhaitées: o pour une pleine
note, \o pour une note blanche, \. pour une note noire, etc...
Soutien d'une note
Le soutien d'une note correspond au délai pendant lequel la note est audible pendant son temps
d'exécution. On définit une valeur sustain qui exprime le pourcentage de soutien d'émission de
la note pendant sa durée totale. Si cette valeur est à 100, les notes s'enchaineraient sans aucun
silence entre les notes.
\ sustain of note, in interval [0..100] 90 value SUSTAIN ledc \ sustain note in interval [0..100] : sustain.note ( -- ) duration SUSTAIN 100 */ ms CHANNEL0 0 ledcWriteTone drop duration 100 SUSTAIN - 100 */ ms ;
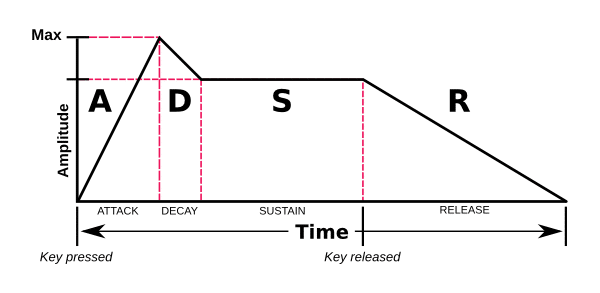
Sur un synthétiseur, l'enveloppe d'un son est déterminé par quatre parties A D S R:
- Attack: marque le début du son
- Decay: suit attack, marque l'écrasement sonore qui précède la partie sustain
- Sustain: marque la partie pendant laquelle le son est soutenu
- Release: marque la partie pendant laquelle le son s'atténue
Dans cet article, les sons que nous générons n'ont qu'une partie sustain.
Le mot sustain.note génère deux délais. Le premier délai correspond à la
durée du maintien de la note. Le second délai correspond à un délai de maintien du silence.
La somme de ces deux délais correspond toujours au délai défini dans duration.
Création des notes musicales
On arrive à la partie la plus intéressante, définir les notes par leur nom:
: create-note
\ compile position in octave
create ( position -- )
,
\ get note frequency in current octave
does>
@ 1- get.note
CHANNEL0 swap ledcWriteTone drop
sustain.note
;
\ notes in english notation
1 create-note C
2 create-note C#
3 create-note D
4 create-note D#
5 create-note E
6 create-note F
7 create-note F#
8 create-note G
9 create-note G#
10 create-note A
11 create-note A#
12 create-note B
\ notes in french notation
1 create-note DO
2 create-note DO#
3 create-note RE
4 create-note RE#
5 create-note MI
6 create-note FA
7 create-note FA#
8 create-note SOL
9 create-note SOL#
10 create-note LA
11 create-note LA#
12 create-note SI
: SIL ( -- )
CHANNEL0 0 ledcWriteTone drop
duration ms
;
forth definitions
En plus des douzes notes, de DO à SI, on définit une notre SIL qui est un silence.
Test des notes
On teste toutes les notes, gammme par gamme:
forth definitions
: music-scale ( -- )
C C# D D# E F F# G G# A A# B
;
initTones
forth also music also
.|
80 to SUSTAIN
OCT1 music-scale
OCT2 music-scale
OCT3 music-scale
OCT4 music-scale
OCT5 music-scale
OCT6 music-scale
Si tout se passe bien, on doit dérouler toutes les notes de musique, par demi-tons, de l'octave 1 à l'octave la plus élevée, ici 6. On ne définit pas d'octave supplémentaire. C'est faisable. Mais les sons émis entrent dans une zone limite pour être audibles.
Rimski KORSAKOV: le vol du bourdon
ceci est un premier test de transposition d'une partition musicale. Pour ce faire, on récupère un morceau musical particulièrement difficile, le VOL DU BOURDON de Rimski KORSAKOV:
Voici la première mesure de la première ligne:
Voici comment on va coder cette première mesure, en notation française:
OCT5 MI RE# RE DO# RE DO# DO OCT4 SI
Ou en notation anglaise:
OCT5 E D# D C# D C# C OCT4 B
Voici comment on code la première ligne de cette partition:
: 1stLine ( -- ) .|" ( duration of a quarter black note ) OCT5 MI RE# RE DO# RE DO# DO OCT4 SI OCT5 DO OCT4 SI LA# LA SOL# SOL FA# FA MI RE# RE DO# RE DO# DO OCT3 SI ;
Toutes mes excuses si j'ai fait des erreurs de traduction de la partition.
A ce stade, il est facile de tester cette ligne musicale:
: flightBumbleBee ( -- )
initTones
1stLine
;
flightBumbleBee
On code deux autres lignes:
: 2ndLine ( -- ) .|" ( duration of a quarter black note ) OCT4 DO OCT3 SI FA# FA SOL# SOL FA# FA MI RE# RE DO# RE DO DO# OCT2 SI OCT3 MI RE# RE DO# RE DO DO OCT2 SI OCT3 MI RE# RE DO# DO FA FA RE# ; : 3rdLine ( -- ) .|" ( duration of a quarter black note ) MI RE# RE DO# DO DO# RE RE# MI RE# RE DO# DO FA FA RE# MI RE# RE DO# DO DO# RE RE# MI RE# RE DO# RE DO DO# OCT2 SI OCT3 ; : flightBumbleBee ( -- ) initTones 1stLine 2ndLine 3rdLine ; flightBumbleBee
On vous laisse coder les trois autres lignes de la partition.
Pour notre part, nous verrons comment maitriser la forme des sons, leur enveloppe...
Legal: site web personnel sans commerce / personal site without seling